How-to simulate Markov chain in R Science 14.04.2014

Introduction

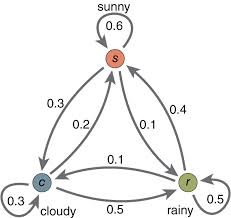
A Markov analysis looks at a sequence of events, and analyzes the tendency of one event to be followed by another. Using this analysis, you can generate a new sequence of random but related events, which will look similar to the original.

A Markov process is useful for analyzing dependent random events - that is, events whose likelihood depends on what happened last. It would NOT be a good way to model a coin flip, for example, since every time you toss the coin, it has no memory of what happened before. The sequence of heads and tails are not inter-related. They are independent events.

But many random events are affected by what happened before. For example, yesterday's weather does have an influence on what today's weather is. They are not independent events.

A Markov model could look at a long sequence of rainy and sunny days, and analyze the likelihood that one kind of weather gets followed by another kind. Let's say it was found that 25% of the time, a rainy day was followed by a sunny day, and 75% of the time, rain was followed by more rain. Let's say we found out additionally, that sunny days were followed 50% of the time by rain, and 50% by sun. Given this analysis, we could generate a new sequence of statistically similar weather by following these steps:

1) Start with today's weather. 2) Given today's weather, choose a random number to pick tomorrow's weather. 3) Make tomorrow's weather "today's weather" and go back to step 2.

What we'd get is a sequence of days like:

Sunny Sunny Rainy Rainy Rainy Rainy Sunny Rainy Rainy Sunny Sunny...

In other words, the "output chain" would reflect statistically the transition probabilities derived from weather we observed.

This stream of events is called a Markov Chain. A Markov Chain, while similar to the source in the small, is often nonsensical in the large. (Which is why it's a lousy way to predict weather.) That is, the overall shape of the generated material will bear little formal resemblance to the overall shape of the source. But taken a few events at a time, things feel familiar.

Math background

If you wanna to see the math background of Markov Chain look at this PDF.

Simulation in R

I'm going to use markovchain package in R. Let's install and load it.

install.packages("markovchain")

library("markovchain")

markovchain objects can be created either in a long way, as the following code shows

weatherStates = c("sunny", "cloudy", "rain")
byRow = TRUE
weatherMatrix = matrix(data = c(0.70, 0.2,0.1,
0.3,0.4, 0.3,
0.2,0.45,0.35), byrow = byRow, nrow = 3,

dimnames = list(weatherStates, weatherStates))

mcWeather = new("markovchain", states = weatherStates, byrow = byRow,
transitionMatrix = weatherMatrix, name = "Weather")

or in a shorter way, as shown below

mcWeather = new("markovchain", states = c("sunny", "cloudy", "rain"),
transitionMatrix = matrix(data = c(0.70, 0.2,0.1,
0.3,0.4, 0.3,
0.2,0.45,0.35),byrow = byRow, nrow = 3),
name = "Weather")

Operations on markovchain objects can can be easily performed. Using the previously defined matrix we can find what is the probability distribution of expected weather states two and seven days after, given actual state to be cloudy.

initialState = c(0,1,0)
after2Days = initialState * (mcWeather * mcWeather)
after7Days = initialState * (mcWeather^7)

after2Days
#    sunny cloudy rain
# [1,] 0.39 0.355 0.255

after7Days
#       sunny    cloudy      rain
# [1,] 0.4622776 0.3188612 0.2188612

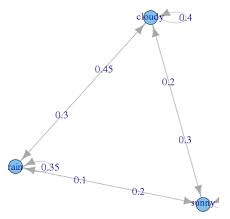
Finally, let's plot Markov chain with weather example.

Useful links

• What's a Markov Process?
• Easy Introduction to Markov Chains in R
• The markovchain Package: A Package for Easily Handling Discrete Markov Chains in R
• About Markov Chain (in Russian)